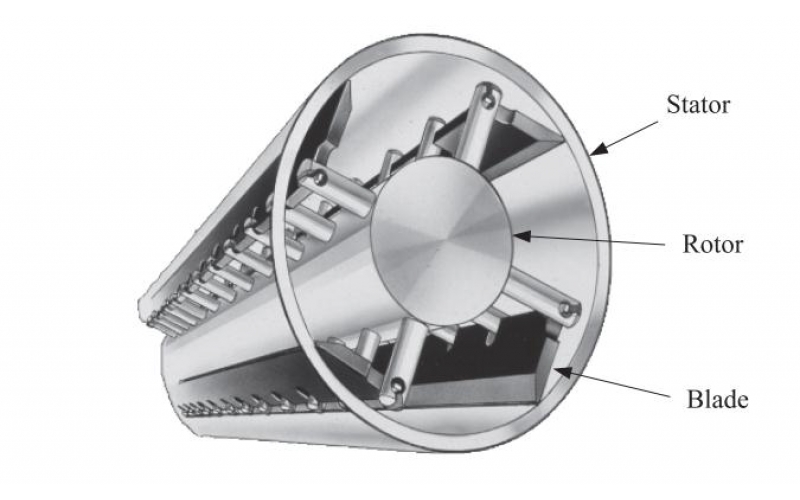
Es wird ein einfaches mathematisches Modell der Flüssigkeitsströmung in einem üblichen Schabewärmetauschertyp vorgestellt, bei dem die Lücken zwischen den Schaufeln und den Gerätewänden eng sind, so dass eine schmierungstheoretische Beschreibung der Strömung gültig ist. Konkret wird die stetige isotherme Strömung einer Newtonschen Flüssigkeit um eine periodische Anordnung schwenkbarer Schaberblätter in einem Kanal mit einer stationären und einer beweglichen Wand analysiert, wenn ein Druckgradient in einer Richtung senkrecht zur Wandbewegung angelegt wird. Die Strömung ist dreidimensional, zerfällt jedoch auf natürliche Weise in eine zweidimensionale „Querströmung“, die durch die Grenzbewegung angetrieben wird, und eine „Längsströmung“, die durch den Druck angetrieben wird. Es werden zunächst Details zur Struktur der Querströmung abgeleitet und insbesondere die Gleichgewichtspositionen der Schaufeln berechnet. Es zeigt sich, dass der gewünschte Kontakt zwischen den Flügeln und der beweglichen Wand erreicht wird, vorausgesetzt, dass die Flügel ausreichend nah an ihre Enden geschwenkt werden. Wenn der gewünschte Kontakt erreicht ist, sagt das Modell voraus, dass die Kräfte und Drehmomente auf die Schaufeln singulär sind, und daher wird das Modell verallgemeinert, um drei zusätzliche physikalische Effekte einzubeziehen, nämlich nicht-newtonsches Potenzgesetzverhalten, Schlupf an starren Grenzen und Kavitation in Regionen mit sehr niedrigem Druck, von denen jede diese Singularitäten nachweislich auflöst. Abschließend wird die Natur der Längsströmung diskutiert.